README

这是一个示例Rubix ML项目，它使用逻辑回归估计器和30,000个信用卡客户样本数据集，预测客户下个月信用卡账单违约的概率。我们还将使用统计学描述数据集，并使用称为t-SNE的流形学习方法对其进行可视化。

难度：中等
训练时间：分钟

安装

使用Composer在本地上传项目

$ composer create-project rubix/credit

要求

PHP 7.4或更高版本

教程

介绍

提供给我们的是包含来自台湾信用卡发行商30,000个标记样本的数据集。我们的目标是训练一个估计器，预测客户下个月信用卡账单的违约概率。由于这是一个二元分类问题（将违约或不会违约），我们可以使用二元分类器逻辑回归，该回归实现概率接口以进行预测。逻辑回归是一个监督学习器，它使用称为梯度下降的算法在内部训练线性模型。

注意：本例的源代码可以在项目根目录下的train.php文件中找到。

提取数据

在Rubix ML中，数据通过专门的容器传递，称为Dataset对象。我们将首先使用内置的CSV提取器提取dataset.csv文件中的数据，然后使用fromIterator()工厂方法从其中实例化一个Labeled数据集对象。

use Rubix\ML\Datasets\Labeled;
use Rubix\ML\Extractors\CSV;

$dataset = Labeled::fromIterator(new CSV('dataset.csv', true));

数据集准备

由于无法从CSV格式推断数据类型，整个数据集将以字符串的形式加载。在继续之前，我们需要将数字类型转换为整数和浮点数。幸运的是，Numeric String Converter可以自动完成这项任务。

性别、教育程度和婚姻状况等分类特征以及年龄和信用额度等连续特征现在已处于适当的格式。然而，逻辑回归估计器不能直接与分类特征兼容，因此我们需要使用One Hot Encode将它们转换为连续的。_One hot_编码将分类特征列的值转换为二进制特征向量，其中表示活动类别的特征高（1），其他所有特征低（0）。

此外，将数据集居中和缩放是一种好的做法，因为它有助于加速梯度下降学习算法的收敛。为此，我们将在数据集上链式另一个转换，称为Z Scale Standardizer，该转换通过将每列除以其Z分数来标准化数据。

use Rubix\ML\Transformers\NumericStringConverter;
use Rubix\ML\Transformers\OneHotEncoder;
use Rubix\ML\Transformers\ZScaleStandardizer;

$dataset->apply(new NumericStringConverter())
    ->apply(new OneHotEncoder())
    ->apply(new ZScaleStandardizer());

我们需要留出一部分数据以便以后用于测试。我们之所以将数据分开，而不是在所有样本上训练学习器，是因为我们希望能够在学习器之前从未见过的样本上测试它。Dataset对象上的stratifiedSplit()方法根据用户指定的比例将数据集公平地分成两个子集。在这个例子中，我们将使用80%的数据进行训练，保留20%用于测试。

[$training, $testing] = $dataset->stratifiedSplit(0.8);

创建学习器实例

您会注意到逻辑回归有几个参数需要考虑。这些参数被称为超参数，因为它们在训练和推理过程中对算法行为有全局影响。在这个例子中，我们将指定前三个超参数，即批量大小和梯度下降优化器及其学习率。

如前所述，逻辑回归使用名为梯度下降的算法进行训练。具体来说，它使用一种名为小批量梯度下降的GD形式，每次通过学习器随机数据集的小批量。批量的大小由批量大小超参数确定。小批量大小通常训练更快，但产生的梯度对于学习器来说更粗糙。在我们的例子中，我们将选择每个批量为256个样本，但您可以根据自己的需要调整此设置。

下一个超参数是GD优化器，它控制算法的更新步骤。大多数优化器都有一个全局学习率设置，允许您控制每次梯度下降步骤的大小。《a href="https://docs.rubixml.com/latest/neural-network/optimizers/step-decay.html" rel="nofollow noindex noopener external ugc">步长衰减优化器会逐步以给定因子减少学习率，每n步从全局设置开始。这允许训练开始时快速，然后随着接近梯度最小值而减慢。我们将选择每100步衰减学习率，起始率为0.01。要创建学习器实例，将超参数传递给逻辑回归构造函数。

use Rubix\ML\Classifiers\LogisticRegression;
use Rubix\ML\NeuralNet\Optimizers\StepDecay;

$estimator = new LogisticRegression(256, new StepDecay(0.01, 100));

设置记录器

由于逻辑回归实现了Verbose接口，我们可以传递一个PSR-3兼容的记录器实例，它将在训练期间将有用的信息记录到控制台。我们将使用与Rubix ML一起构建的Screen记录器，但您也可以选择任何优秀的PHP记录器，如Monolog或Analog来完成这项工作。

use Rubix\ML\Other\Loggers\Screen;

$estimator->setLogger(new Screen());

训练

现在，您可以通过将之前创建的训练集传递给学习器实例上的train()方法来训练学习器。

$estimator->train($dataset);

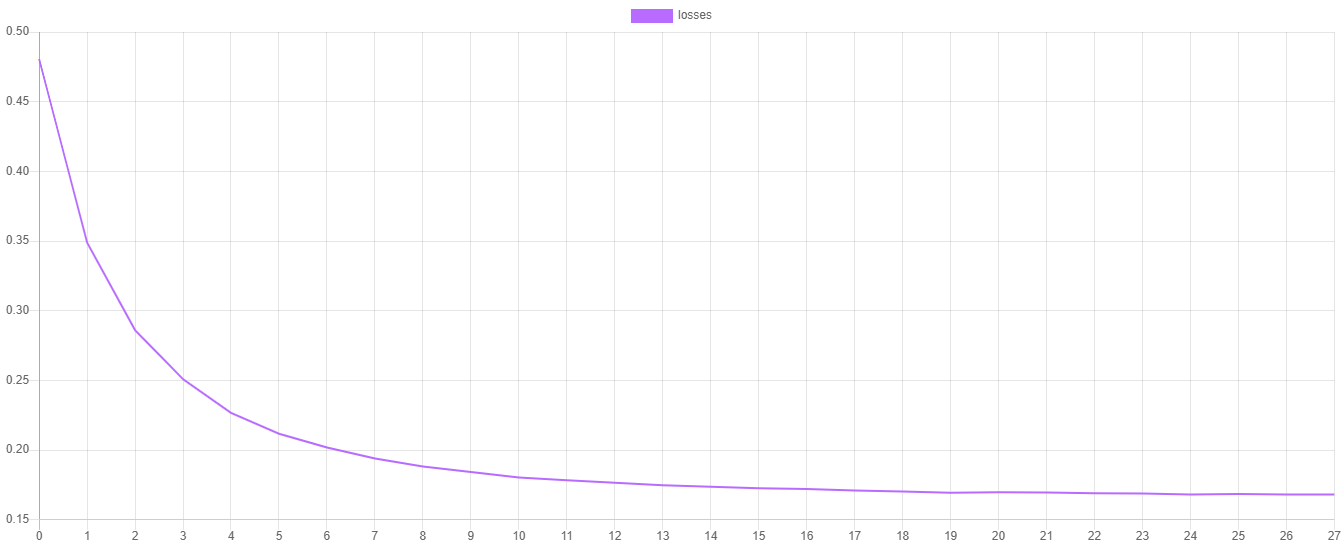
训练损失

逻辑回归中的 steps() 方法输出了上次训练会话每个时期交叉熵代价函数的值。交叉熵代价函数的值可以通过将它们导出到CSV文件，然后导入您喜欢的绘图软件（如Plotly或Tableau）来绘制。

use Rubix\ML\Extractors\CSV;

$extractor = new CSV('progress.csv', true);

$extractor->export($estimator->steps());

您会注意到损失值在每个时期都应该在下降，并且随着学习者接近代价函数最小值的收敛，损失值的改变应该越来越小。

交叉验证

一旦学习者被训练，下一步就是确定最终的模型能否很好地泛化到现实世界。为此，我们需要之前留出的测试数据。我们将继续生成两个报告，这些报告将比较估计器输出的预测与测试集中的真实标签。

多分类分解报告为我们提供了关于模型在每个类别层面性能的详细指标（准确率、F1分数、MCC）。此外，混淆矩阵是一个表格，比较了特定类别的预测数量与实际的真实值。我们可以将这两个报告封装在一个综合报告中，以同时生成它们。

use Rubix\ML\CrossValidation\Reports\AggregateReport;
use Rubix\ML\CrossValidation\Reports\MulticlassBreakdown;
use Rubix\ML\CrossValidation\Reports\ConfusionMatrix;

$report = new AggregateReport([
    new MulticlassBreakdown(),
    new ConfusionMatrix(),
]);

要为报告生成预测，请在估计器上调用具有测试集的predict()方法。

$predictions = $estimator->predict($testing);

然后，通过在报告实例上调用generate()方法来生成带有预测和标签的报告。

$results = $report->generate($predictions, $testing->labels());

现在我们可以执行训练脚本并查看验证结果。

$ php train.php

报告的输出应该类似于下面的输出。在这个例子中，我们的分类器准确率为83%，F1分数为0.69。此外，混淆矩阵表显示，每次我们预测yes时，我们正确了471次，错误了170次。

[
    {
        "overall": {
            "accuracy": 0.8288618563572738,
            "precision": 0.7874506659370852,
            "recall": 0.6591447375205939,
            "specificity": 0.6591447375205939,
            "negative_predictive_value": 0.7874506659370852,
            "false_discovery_rate": 0.21254933406291476,
            "miss_rate": 0.3408552624794061,
            "fall_out": 0.3408552624794061,
            "false_omission_rate": 0.21254933406291476,
            "f1_score": 0.6880266172924424,
            "mcc": 0.42776751059741475,
            "informedness": 0.31828947504118776,
            "markedness": 0.5749013318741705,
            "true_positives": 4974,
            "true_negatives": 4974,
            "false_positives": 1027,
            "false_negatives": 1027,
            "cardinality": 6001
        },
        "classes": {
            "yes": {
                "accuracy": 0.8288618563572738,
                "precision": 0.734789391575663,
                "recall": 0.3546686746987952,
                "specificity": 0.9636208003423925,
                "negative_predictive_value": 0.8401119402985074,
                "false_discovery_rate": 0.26521060842433697,
                "miss_rate": 0.6453313253012047,
                "fall_out": 0.0363791996576075,
                "false_omission_rate": 0.15988805970149256,
                "f1_score": 0.47841543930929414,
                "informedness": 0.31828947504118776,
                "markedness": 0.5749013318741705,
                "mcc": 0.42776751059741475,
                "true_positives": 471,
                "true_negatives": 4503,
                "false_positives": 170,
                "false_negatives": 857,
                "cardinality": 1328,
                "density": 0.22129645059156808
            },
            "no": {
                "accuracy": 0.8288618563572738,
                "precision": 0.8401119402985074,
                "recall": 0.9636208003423925,
                "specificity": 0.3546686746987952,
                "negative_predictive_value": 0.734789391575663,
                "false_discovery_rate": 0.15988805970149256,
                "miss_rate": 0.0363791996576075,
                "fall_out": 0.6453313253012047,
                "false_omission_rate": 0.26521060842433697,
                "f1_score": 0.8976377952755906,
                "informedness": 0.31828947504118776,
                "markedness": 0.5749013318741705,
                "mcc": 0.42776751059741475,
                "true_positives": 4503,
                "true_negatives": 471,
                "false_positives": 857,
                "false_negatives": 170,
                "cardinality": 4673,
                "density": 0.7787035494084319
            }
        }
    },
    {
        "yes": {
            "yes": 471,
            "no": 170
        },
        "no": {
            "yes": 857,
            "no": 4503
        }
    }
]

探索数据集

探索性数据分析是使用统计和散点图等分析技术来更好地了解数据的过程。在本节中，我们将使用统计描述信用卡数据集的特征列，然后绘制数据集的低维嵌入以可视化其结构。

注意：本例的源代码可以在项目根目录中的explore.php文件中找到。

首先，导入信用卡数据集并转换与之前步骤相同的数值字符串。

use Rubix\ML\Datasets\Labeled;
use Rubix\ML\Extractors\CSV;
use Rubix\ML\Transformers\NumericStringConverter;

$dataset = Labeled::fromIterator(new CSV('dataset.csv', true))
    ->apply(new NumericStringConverter());

描述数据集

我们实例化的数据集对象有一个describe()方法，该方法为数据集中的每个特征列生成统计信息。将为每个分类特征值计算类别密度，并将输出连续特征列的均值、中位数和标准差等统计信息。返回值是一个报告对象，可以被输出到终端。

$stats = $dataset->describe();

echo $stats;

以下是信用卡数据集前两列的输出。我们可以看到，第一列credit_limit的均值为167,484，值的分布向左倾斜。我们还知道第二列gender包含两个类别，并且在这个数据集中女性多于男性（60 / 40）。自行生成并检查数据集的统计信息，看看您是否能识别出数据集的其他有趣特征。

[
    {
        "type": "continuous",
        "mean": 167484.32266666667,
        "variance": 16833894533.632648,
        "std_dev": 129745.49908814814,
        "skewness": 0.9928173164822339,
        "kurtosis": 0.5359735300875466,
        "min": 10000,
        "25%": 50000,
        "median": 140000,
        "75%": 240000,
        "max": 1000000
    },
    {
        "type": "categorical",
        "num_categories": 2,
        "densities": {
            "female": 0.6037333333333333,
            "male": 0.39626666666666666
        }
    }
]

此外，我们还会将统计数据保存到JSON文件中，以便以后参考。

use Rubix\ML\Persisters\Filesystem;

$stats->toJSON()->saveTo(new Filesystem('stats.json'));

数据集可视化

信用卡数据集有25个特征，经过独热编码后变为93个。因此，这个数据集的向量空间是93维的。用肉眼来可视化这种高维数据，只能通过将维度数量减少到可以在图表上绘制的内容（1-3维）来实现。这种降维方法称为流形学习，因为它试图找到数据的一个低维流形。在这里，我们将使用一个流行的流形学习算法，即t-SNE，通过将其嵌入到仅两个维度来帮助我们可视化数据。

我们不需要整个数据集来生成一个不错的嵌入，所以我们会从数据集中抽取2500个随机样本，并仅嵌入这些样本。数据集对象的head()方法将返回数据集中前n个样本和标签的新数据集对象。在事先随机化数据集将消除数据收集和插入的顺序偏差。

use Rubix\ML\Datasets\Labeled;

$dataset = $dataset->randomize()->head(2500);

实例化嵌入器

t-SNE代表t-Distributed Stochastic Neighbor Embedding，是一种适用于可视化高维数据集的强大非线性降维算法。第一个超参数是目标嵌入的维度数。由于我们希望能够以二维散点图的形式绘制嵌入，我们将此参数设置为整数2。下一个超参数是学习率，它控制嵌入器更新目标嵌入的速度。我们将设置的最后一个超参数称为困惑度，可以理解为在计算样本分布的方差时考虑的最近邻的数量。请参阅文档以了解超参数的完整描述。

use Rubix\ML\Embedders\TSNE;

$embedder = new TSNE(2, 20.0, 20);

嵌入数据集

在我们继续之前，我们需要准备数据集以进行嵌入，因为与逻辑回归一样，t-SNE只与连续特征兼容。我们可以通过将转换器传递到数据集对象的apply()方法来执行数据集上必要的转换，就像我们在教程中之前所做的那样。

use Rubix\ML\Transformers\OneHotEncoder;
use Rubix\ML\Transformers\ZScaleStandardizer;

$dataset->apply(new OneHotEncoder())
    ->apply(new ZScaleStandardizer());

注意：使用Z Scale Standardizer或其他标准化器对数据进行居中和标准化并不总是必要的，但是，恰好逻辑回归和t-SNE在数据居中和标准化时都会受益。

由于嵌入器本质上是一个转换器，您可以使用新实例化的t-SNE嵌入器，使用apply()方法将样本嵌入到数据集中。

$dataset->apply($embedder);

嵌入完成后，我们可以将数据集保存到文件中，以便以后在我们的 favorite plotting software中打开。

use Rubix\ML\Extractors\CSV;

$dataset->exportTo(new CSV('embedding.csv'));

现在我们准备好执行探索脚本，并使用我们 favorite plotting software绘制嵌入。

$ php explore.php

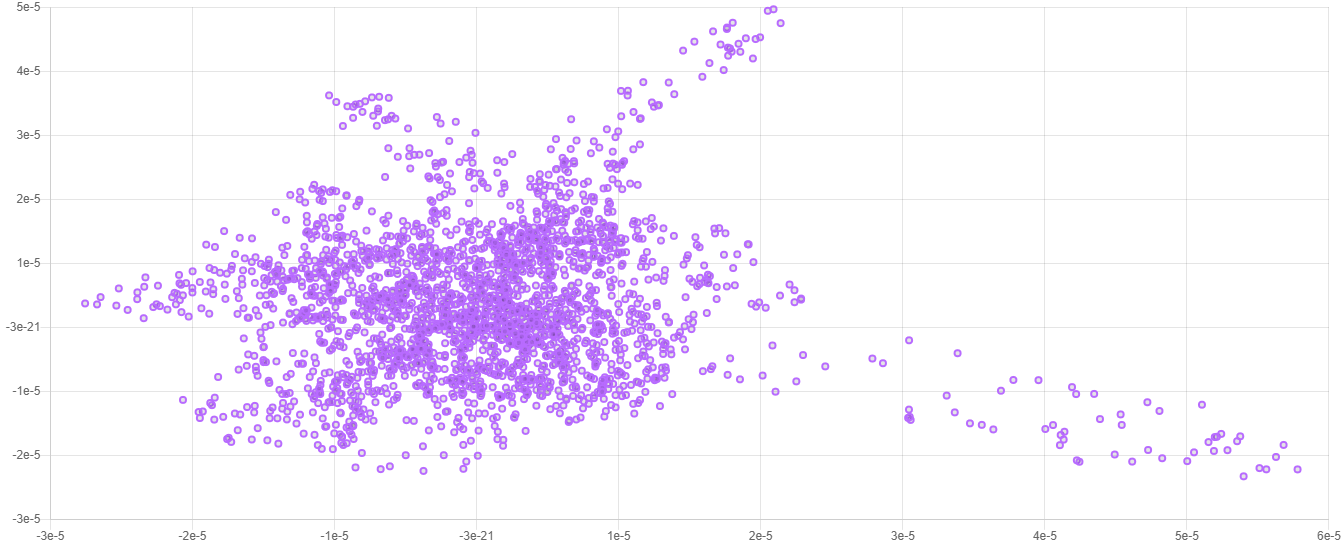
以下是典型二维嵌入在绘图中的示例。

注意：由于t-SNE算法的随机性，每次嵌入都会略有不同。重要的信息包含在数据的整体结构中。

下一步

恭喜您完成了教程！我们刚刚训练的逻辑回归估计器能够实现与原始论文相同的结果，然而，Rubix ML中有其他估计器可以选择，可能表现更好。考虑使用集成方法，如AdaBoost或随机森林作为下一步。

幻灯片

如需额外帮助或更深入地了解逻辑回归、梯度下降和交叉熵损失函数背后的数学原理，您可以参考随此示例项目附带的幻灯片集。

原始数据集

联系人：叶一成邮箱：(1) icyeh '@' chu.edu.tw (2) 140910 '@' mail.tku.edu.tw
机构：(1) 台湾中华大学信息管理系。 (2) 台湾淡江大学土木工程系。其他联系方式：886-2-26215656转3181

参考文献

叶一成，李建和. (2009). 比较数据挖掘技术在预测信用卡客户违约概率中的预测准确率. 专家系统与应用，36(2)，2473-2480.

Dua, D. 和 Graff, C. (2019). UCI机器学习库 [http://archive.ics.uci.edu/ml]. 加利福尼亚州欧文：加州大学信息与计算机科学学院。

许可证

代码采用MIT许可证，教程采用CC BY-NC 4.0许可证。

rubix / credit

维护者

详细信息