README

俄语版本

目录

• 介绍
• 演示
• 安装
• 如何使用
• 设置
• 性能
• TSPLIB95
• 术语

介绍

蚁群优化是一种概率技术，用于解决可以归结为在图中找到良好路径的计算问题（来自维基百科）。

我们正在解决的问题可以是“旅行商问题”或“最短路径问题”，或约束最短路径优先等。
这两个任务在这个库中得以解决。

经典蚁群算法有许多策略和变体。
这个库直接实现了经典蚁群算法和具有精英蚁的蚁群算法。

这个库可以很容易地扩展，以便您可以实现自己的蚁群算法变体，并解决您需要的任务。

图的初始数据要么来自邻接矩阵，要么来自具有其X和Y坐标的节点列表（城市、顶点等）。

这个库的工作已经与TSPLIB95数据集进行了测试，因此我们可以检查其性能和效率。

蚂蚁的数量、所有系数和参数都可以根据需要更改。

现在我们有一个Web应用，您可以安装并本地运行以练习此算法。请查看其视频演示以获取详细信息。

演示

使用蚁群优化算法解决旅行商问题：

另一个示例：

安装

通过composer安装：

安装此库的首选方法是使用composer。

运行以下命令：

composer require --prefer-dist mgrechanik/ant-colony-optimization

或将以下内容添加到您的composer.json文件的require部分：

"mgrechanik/ant-colony-optimization" : "~1.0.0"

如何使用

基本API

使用所需依赖项创建Manager

1.       - 默认情况下，Finder将是经典类型，而Task将是旅行商问题

Manager::__construct(DistanceInterface $distanceStrategy = null, AFinder $finder = null, 
                     MathematicsInterface $mathematics = null, Task $task = null);

      - $nameStart - 从哪个数字开始命名节点的别名

1. 从邻接矩阵加载数据

$manager->setMatrix(array $matrix, int $nameStart = 0)

      - $nameStart - 从哪个数字开始命名节点的别名

1. 从城市数组加载数据

$manager->setCities(City ...$cities)

      - 此城市数组将被转换为邻接矩阵。距离将根据我们为Manager设置的策略计算。
      - 如果城市具有name属性，它将成为其别名

1. 更改邻接矩阵

$manager->updateMatrix(int $y, int $x, float|int $value, bool $double = true)

      - 例如，我们可以使某些路径不可通行 - $manager->updateMatrix(1, 0, 1000000);

1. 运行计算过程

$distance = $manager->run(int $iterations = 400)

      - 对于小图，我们可以减少迭代次数。
      - 它将返回找到的距离或搜索无结果时返回 null

1. 获取找到的路径

$path = $manager->getInnerPath()

      - 我们找到的路径，由节点的编号组成。
      所有节点都内部命名为从0到N-1的数字，其中N是节点数量。

1. 获取别名路径

$path = $manager->getNamedPath()

      - 如果我们设置它们，我们将找到由节点名称别名组成的路径。

示例

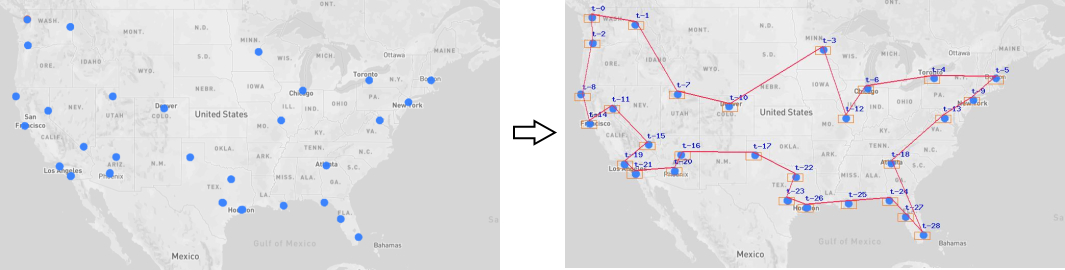
使用经典ACO解决“旅行商问题”

use mgrechanik\aco\Manager;

$manager = new Manager();
$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ],
            [11, 5, 8, 0 ]
          ];
$manager->setMatrix($matrix);
$distance = $manager->run(20);
var_dump('Distance=' . $distance);
var_dump($manager->getInnerPath())

我们将得到

Distance=25

Array
(
    [0] => 0
    [1] => 1
    [2] => 3
    [3] => 2
    [4] => 0
) 

使用经典ACO解决“最短路径问题”

use mgrechanik\aco\Manager;
use mgrechanik\aco\SppTask;

$task = new SppTask(0, 3);
$manager = new Manager(task : $task);
$matrix = [
            [ 0 , 8, 4, 100],
            [ 8 , 0, 9, 5  ],
            [ 4 , 9, 0, 8  ],
            [100, 5, 8, 0  ]
          ];
$manager->setMatrix($matrix);   
$finder = $manager->getFinder();
// increase amount of ants to 6
$finder->setM(6);
$distance = $manager->run(50);
var_dump('Distance=' . $distance);
var_dump($manager->getInnerPath())

我们将得到

Distance=12

Array
(
    [0] => 0
    [1] => 2
    [2] => 3
)
// for comparison, the direct path [0, 3] is closed by big distance and distance of path [0, 1, 3] is 13

将数据作为城市数组加载

use mgrechanik\aco\Manager;
use mgrechanik\aco\City;

$cities = [new City(10,10), new City(50,50), new City(10,50), new City(60,10)];
$manager = new Manager();
$manager->setCities(...$cities);

将数据作为邻接矩阵加载

use mgrechanik\aco\Manager;

$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ] ,
            [11, 5, 8, 0 ]
          ];
$manager = new Manager();
$manager->setMatrix($matrix);

使用精英搜索器

$finder = new \mgrechanik\aco\elitist\Finder();
$manager = new Manager(finder : $finder);
//...

查看我们工作的历史 - 我们找到的最好解决方案

use mgrechanik\aco\Manager;

$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ] ,
            [11, 5, 8, 0 ]
          ];
$manager = new Manager();
$finder = $manager->getFinder();
$manager->setMatrix($matrix);
$manager->run();
var_dump($finder->getHistory());

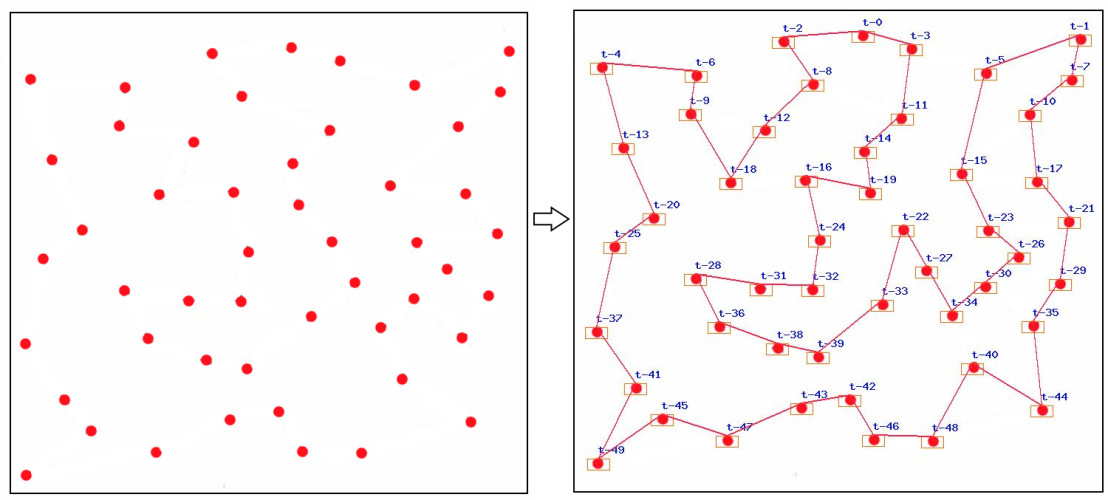
从图像文件加载城市列表

使用此库，我们可以从图像中加载城市列表。搜索结果也可以显示在图像上。它看起来像演示中的图像。

阅读该库的文档以获取更多有关如何准备图像的信息，但简要来说是这样的：在白色画布上绘制直径为10 px的点（它们是图的顶点）并使用下面的代码与这张图像一起使用

use mgrechanik\aco\Manager;
use mgrechanik\aco\City;

try {
    $imageSearcher = new \mgrechanik\imagepointssearcher\Searcher(
        './images/your_image.jpg',
    );
    $found = $imageSearcher->run();    
    if ($found > 1) {
        $points = $imageSearcher->getPoints();
        $cities = [];
        foreach ($points as $point) {
            $cities[] = new City($point['x'], $point['y']);
        }    
        $manager = new Manager();
        $manager->setCities(...$cities);
        if ($res = $manager->run()) {
            $innerPath = $manager->getInnerPath();
            $imageResult = new \mgrechanik\imagepointssearcher\ImageResult($imageSearcher);
            $imageResult->drawLabels();
            $imageResult->drawMargins();
            $imageResult->drawPath($innerPath);
            $imageResult->save('./images/result.jpg');
        }
    }
  
} catch (Exception $e) {
    //
}

设置

搜索器设置

我们调整的基础对象是搜索器。
让我们获取它

$manager = new Manager();
$finder = $manager->getFinder();
// Settings
//$finder->set...
// ...
//$manager->run();

可用的设置

• 设置使两个节点之间的路径不可通行的距离值
  ->setClosedPathValue(int $value)

• 设置蚂蚁的数量
  ->setM(int $m)

• 设置蚂蚁的数量占节点数量的百分比。默认行为（=40%）
  ->setMPercent(int $mPercent)

• 设置公式的系数

->setAlpha(float $alpha);
->setBeta(float $beta);
->setP(float $p);
->setC(float $c);
->setQ(int $q);

• 设置进行数学工作的策略
  ->setMathematics(MathematicsInterface $mathematics)

• 设置我们正在解决的问题。例如TSP，SPP或其他。
  ->setTask(Task $task)

• 设置精英蚂蚁的数量（当使用精英搜索器时）
  ->setSigma(int $sigma)

• 设置精英蚂蚁占常规蚂蚁数量的百分比。默认行为（=50%）（当使用精英搜索器时）
  ->setSigmaPercent(int $sPercent)

性能

首先，关闭XDebug或其类似项，因为它们可能会显著影响算法的工作时间

此ACO算法在图上找到良好的路径。有时甚至是最佳路径。

让我们以TSPLIB95库中的berlin52.tsp任务为例，它有52个节点。
使用以下代码解决这个问题

$cities = TspLibLoader::loadCitiesFromEuc2dFile(__DIR__ . '/images/data/berlin52.tsp');
$finder = new \mgrechanik\aco\elitist\Finder();
$finder->setSigmaPercent(150);
$finder->setMPercent(30);
$finder->setAlpha(0.7);
$manager = new Manager(finder : $finder);
$manager->setCities(...$cities);
$distance = $manager->run(300);
var_dump('Distance=' . $distance);
var_dump($finder->getHistory());

我们将看到

Distance=7542

   Array ... 
    [85] => Array
        (
            [distance] => 7542
            [inner_path] => 0_21_30_17_2_16_20_41_6_1_29_22_19_49_28_15_45_43_33_34_35_38_39_36_37_47_23_4_14_5_3_24_11_27_26_25_46_12_13_51_10_50_32_42_9_8_7_40_18_44_31_48_0
            [iteration] => 85
            [time_spent] => 1.94 sec
        )  
    )

此代码在办公室电脑上运行，在不到2秒的时间内找到了已知的最短路径。

我们在这里使用了精英ACO算法，因为在实践中它比经典算法给出更好的结果。

算法是概率性的，蚂蚁在每次新的搜索中都会以不同的方式旅行。许多因素取决于节点的数量、蚂蚁的数量以及用于公式的所有系数和参数。

TSPLIB95

TSPLIB95库附带了许多旅行商问题 - 初始数据和解决方案 - 这些任务的最佳结果（路径和距离）。

该库非常有价值，我们可以使用它的数据来测试我们算法、系数和参数的效率。

该库包含许多不同的初始数据格式。开箱即用，我们支持其中两种。

以城市坐标的X和Y坐标集合的形式加载数据。距离是欧几里得距离。

此格式的文件示例 - berlin52.tsp。
加载节点（城市）列表并将其传输到Manager

use mgrechanik\aco\TspLibLoader;
use mgrechanik\aco\Manager;

$fileName = __DIR__ . '/berlin52.tsp';
$cities = TspLibLoader::loadCitiesFromEuc2dFile($fileName);
$manager = new Manager();
$manager->setCities(...$cities);

将数据作为邻接矩阵加载

此格式的文件示例 - bays29.tsp。
加载邻接矩阵并将其传输到Manager

use mgrechanik\aco\TspLibLoader;
use mgrechanik\aco\Manager;

$fileName = __DIR__ . '/bays29.tsp';
$matrix = TspLibLoader::loadMatrixFromExplicitMatrixFile($fileName);
$manager = new Manager();
// tsplib95 library names nodes starting with "1"
$manager->setMatrix($matrix, 1);

术语

ACO - 蚁群优化算法

节点 - 节点、顶点或城市。蚂蚁在它们之间移动。

邻接矩阵 - 邻接矩阵设置图节点之间的距离。这是我们算法开始工作的基本结构。

当以带有坐标的城市（Cities）的形式加载图时，此信息将转换为邻接矩阵。

经典寻找者 - 实现经典ACO算法的寻找者

精英寻找者 - 当我们使用精英蚂蚁时实现ACO算法的寻找者

蚂蚁 - 蚂蚁，工作单元，它们在图中移动以寻找路径

任务 - 我们在图上解决的问题。例如，可能是“旅行商问题”或“最短路径问题”。或其它。

TSP - 旅行商问题。使用此库我们可以解决对称和非对称类型的TSP

Manager - 管理器，其任务是形成邻接矩阵，将其提供给Finder以解决任务。

迭代 - 所有蚂蚁找到一条路径并放置信息素的过程。我们自行设置迭代次数。

信息素 - 蚂蚁在路径上留下的实例

m - 蚂蚁的数量

mPercent - 相对于节点数量的蚂蚁百分比

sigma - 如果使用相应算法，精英蚂蚁的数量

sigmaPercent - 相对于普通蚂蚁数量的精英蚂蚁百分比

alpha - 控制信息素数量影响的系数

beta - 控制路径吸引力的系数

p - 蒸发系数

c - 路径上初始信息素的量

Q - 计算蚂蚁在找到的路径上放置的信息素数量的常数