README

安装

通过composer

composer require lmn/subsetsum

概述

wikipedia

该算法仅适用于目标和集合值均为正整数的情况。

复杂度

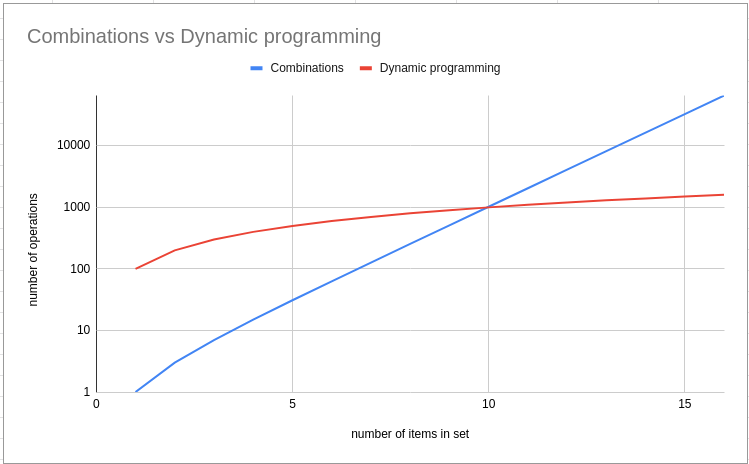
我们将此算法与尝试所有可能组合的算法进行比较。在这种情况下，复杂度是指数级的。

如果我们使用动态规划，我们将得到伪多项式复杂度 O(n * m)，其中 n 是源集中项目的数量，m 是目标增量数量。

操作次数是对数尺度的。计算所有组合似乎线性，但在对数尺度上意味着它是指数增长的。同样适用于动态规划，它可能看起来是对数的，但在对数尺度上它可能是线性的或多项式的（在这种情况下它是线性的，因为目标增量的数量是固定的数字 = 100）

API

我们建议使用 SubsetSumBuilder 生成子集。要创建构建器，只需调用 SubsetSum::builder() 静态方法。

<?php
$subsetTable = SubsetSum::builder()
    ->withSet([1, 2, 5])
    ->withTarget(8)
    ->build();

$subset = $subsetTable->getSubset(8);
?>

如果您喜欢以其他方式创建子集表，您也可以使用SubsetSum类的其他静态方法，例如 SubsetSum::create 和 SubsetSum::createWithRepetition。

值集合

通过调用构建器的 withSet 方法提供子集使用的可能值的集合。

<?php
$subsetTable = SubsetSum::builder()
    ->withSet([1, 2, 5])
    ...
?>

目标

仅计算最大目标值。您必须通过调用 withTarget 方法定义此最大目标值。此方法接受一个参数，即最大目标值。要定义表的最高目标，请用最大目标值的第一参数调用 withTarget 方法，并用目标间隔的第二参数。

<?php
$subsetTable = SubsetSum::builder()
    ->withTarget(800)
    ...
?>

为了优化计算，我们尝试使用 ext-gmp PHP 扩展。如果此扩展不存在，则子集计算仍然正确，但不会完全优化。要手动优化此算法，请参阅下面的段落。

如果您不想安装 ext-gmp PHP 扩展，并且希望尽可能优化您的算法，则可以手动设置计算目标的间隔。使用构建器的 withTargetSpaced 方法。间隔应该是集合值和最终目标的最大公约数。

<?php
$subsetTable = SubsetSum::builder()
    ->withTargetSpaced(800, 100)
    ...
?>

此示例将创建间隔为100的目标 {0, 100, 200, 300, 400, 500, 600, 700, 800}

您还可以通过调用构建器的 withTargetSet 方法指定不均匀间隔的自定义目标集。

<?php
$subsetTable = SubsetSum::builder()
    ->withTargetSet([1, 2, 3, 5, 8, 13, 21, 34])
    ...
?>

创建子集和

要创建子集和表，请调用构建器的 build 方法；

<?php
$subsetTable = SubsetSum::builder()
    ...
    ->build();
?>

创建具有重复的子集和表

要创建具有重复的子集和表，请调用构建器的 buildWithRepetition 方法；

<?php
$subsetTable = SubsetSum::builder()
    ...
    ->buildWithRepetition();
?>

仅查找精确匹配

有时您可能希望仅在子集与目标值完全匹配时找到子集。您可以使用构建器的 onlyExactSum 方法。如果找不到精确匹配，则在调用 $subsetTable->getSubset(); 后将收到空数组。

<?php
$subsetTable = SubsetSum::builder()
    ...
    ->onlyExactSum();
?>

计算结果子集

要从表中计算子集，请调用子集表的 getSubset 方法。此方法将返回一个值数组（子集），可以用于求和以得到最大目标值。

<?php
$subsetTable = SubsetSum::builder()->...->build();

$subset = $subsetTable->getSubset()
?>

要接收小于最大目标值的目标的子集，您可以调用 getSubsetForTarget 并将目标值作为参数传递。

<?php
$subsetTable = SubsetSum::builder()->...->build();

$subset = $subsetTable->getSubsetForTarget(100)
?>

自定义比较函数

有时您可能想更改决定最佳单元值的算法。要更改此决策函数，请使用实现Comeparable接口的类的参数调用构建器的withComperable方法。

您还可以使用构建器的withComparableFunction方法，并传递一个回调参数。

<?php
$subsetTable = SubsetSum::builder()
    ->withComperable(new CustomComperable())
    ...
?>

Builder提供了一些预定义的可比较对象。

• 优先选择较大的
• 优先选择较小的

优先选择较大的

要选择等于或大于目标的一个子集，请使用构建器的preferGreaterSum方法

<?php
$subsetTable = SubsetSum::builder()
    ->preferGreaterSum()
    ...
?>

优先选择较小的

要选择等于或小于目标的子集，请使用构建器的preferLowerSum方法

<?php
$subsetTable = SubsetSum::builder()
    ->preferLowerSum()
    ...
?>

算法

要在多项式时间内计算子集和，您必须使用动态规划。这种方法将在O(n * m)时间内找到子集，其中n是源集中物品的数量，m是目标增量数。

假设您想找到一个等于100的子集，并且您只能使用集合setOfValues = {10, 20, 50, 70}中的值。您会将目标分解成更小的部分，实际上，您会想使用这些值的最大公约数来创建这些较小的目标部分。在这个例子中，GCD将是10，我们的目标部分将看起来像这样setOfTargets = {0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100}。因此，我们的n将等于count(setOfValues) == 4，而我们的m将等于count(setOfTargets) == 11。

在这种情况下，计算值集合的所有组合（4 * 3 * 2 * 1 = 24）比我们的方法（11 * 4 = 44）更快。如果值集合变得更大，我们将看到我们方法的优点。

对于子集和

要计算不重复的子集和，我们必须创建一个表格，其中行是集合中的项目，列是目标部分。我们将从上到下、从左到右填写这个表格。换句话说，我们将遍历每一行，并对每一行遍历每一列。

单元值等于我们当前填充的行可以接近目标数字的程度。所以如果单元值是0，这意味着我们可以创建一个子集，其和等于列值。如果单元值是10，这意味着我们可以创建一个子集，其和比列值小10。我们将使用以下算法填写单元值

• 从当前单元格的列值和行值中减去，称为余数。这是一个假设最佳结果可以通过只使用大小为1的子集来完成的场景。这个子集中的唯一项目是当前行的值。
• 如果余数大于0，则从值余数的上一行的列中取值。称这个值为余数优化。这是一个创建具有当前行值和最佳余数子集的场景。
• 最后一个值是当前列和上一行的单元格。称为跳过当前。这是一个我们不希望将当前行值包含在最终子集中，并期望通过只使用前几行来获得更好的结果的场景。

比较这三个值（余数、余数优化和跳过当前），选择最佳值。在这种情况下，我们将选择最接近零的值。

对于可重复的子集和

为了创建一个可以重复项的子集，我们需要翻转表轴。现在我们将使用集合项作为列，目标值作为行。假设目标值总是多于集合值。这给我们提供了在最终子集中重复集合值的机会。我还会包括一个best列。这只是一个视觉引导，帮助你理解算法的工作原理。这个列在数据结构中实际上并不存在。

填充表格基本上与填充经典子集表相同。我们将遍历每一行，并对每一行遍历每一列。当行被填满时，我们将填充当前行的最佳列。最佳列只是存储一行中的最佳结果。我们只考虑两个值

• 减去当前单元格的列值和行值。我们称之为remainder。这是一个假设最佳结果可以通过仅使用大小为1的子集完成的场景。这个子集中的唯一项将是当前列的值。
• 如果余数大于0，则从remainder行的最佳列中取值。这是一个将当前列值添加到remainder目标最佳子集中的场景。我们称这个值为remainder optimized

当前单元格将拥有这两个值中较好的一个。在这种情况下，我们将选择最接近零的值。当行被填满时，我们将用行中的最佳值填充最佳列。