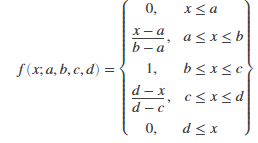README

安装

composer require ketili/fuzzydm

简介

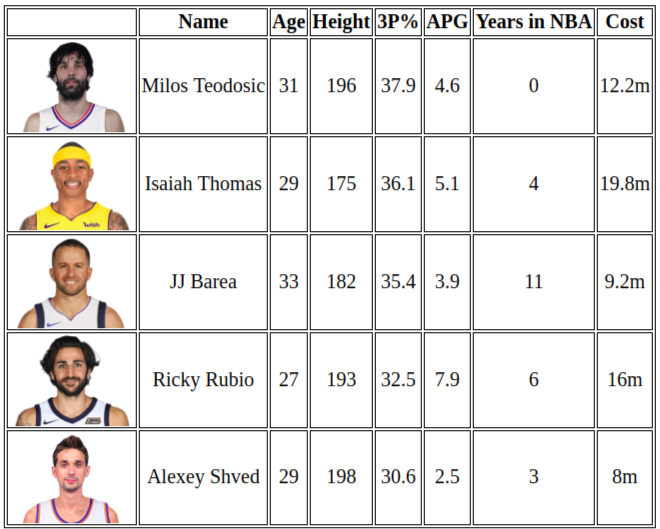
这是一个小巧的PHP库，用于多标准决策。它基于模糊逻辑基础，并使用简单的 隶属度 和 聚合 函数。使用这个库，您可以根据一些预定义的数值特征做出决策。例如，您是某个篮球队的经理，您想为球队进行有利可图的后卫转会，并且您有一些具体要求：您有有限的转会预算，有一些关于体重、年龄或身高的范围，需要尽可能多的经验丰富且年轻的球员。这个例子将在上面讨论，同时还会介绍库中的方法和函数。

示例

让我们想象我们有一份以下守门员列表及其特征：

1. 年龄

您需要一个年轻的球员，那么大约多好的年龄既年轻又有一些经验呢？我认为是24、25或26岁...或者更接近这些数字的年龄。让我们做一个隶属度函数来表达您的需求。如果我们使用梯形隶属度函数会更好，它实际上看起来像

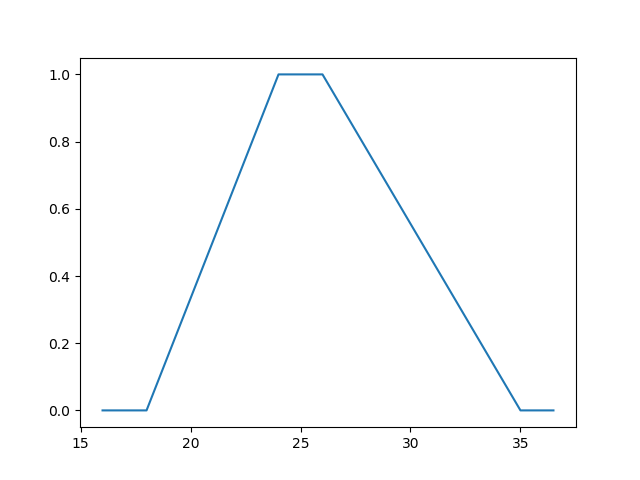
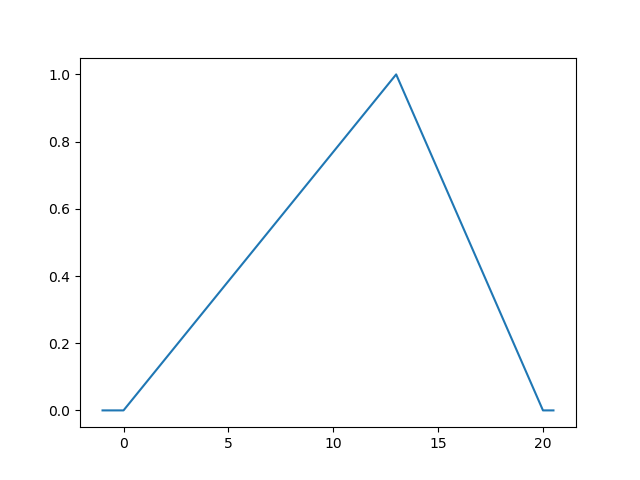
其中a、b、c和d是数值参数，表示梯形图形的角。如果我们依次取a、b、c和d为18、24、26、35，我们会得到这样的图形

这意味着对我们来说，理想的选择是年龄在[24, 26]之间，函数返回1。当自变量接近18和35时，函数的返回值会减少，如图所示。这意味着您不需要18岁的球员，他们没有任何经验，也不需要超过35岁的球员，这对您的球队来说太老了。例如，这个函数将30岁的球员评估为0.55。

2.NBA生涯年数

这里我们使用 三角形隶属度函数

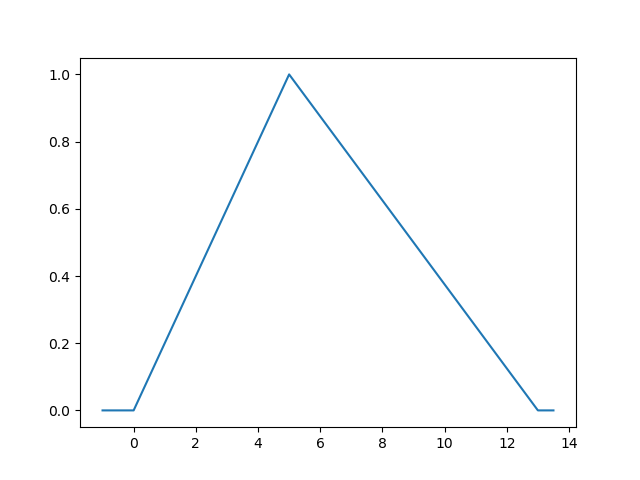
其中a、b和c是数值参数，表示三角形图形的角

在这个图中，a = 0，b = 5，c = 13，这意味着您最喜欢的球员应该是有5年NBA经验的球员。

3.成本

您只有2000万美元，您不想浪费所有的钱，但也不需要购买廉价的球员，因为在市场上成本意味着球员效率。所以我们再次使用 三角形函数，参数为a = 0，b = 13和c = 20

4.身高

当然，控球后卫不高，因为他们应该快速移动，快速运球，并且有良好的运球技巧。以下是维基百科的片段

在NBA中，控球后卫通常身高约为6'3"（1.93米）或更矮，平均身高约为6'2"（1.88米），而在WNBA中，控球后卫通常身高为5'9"（1.75米）或更矮。具有以上平均尺寸（身高、肌肉）被认为是有利的，尽管尺寸是次要的，其次是情境意识、速度、敏捷性和控球技巧。

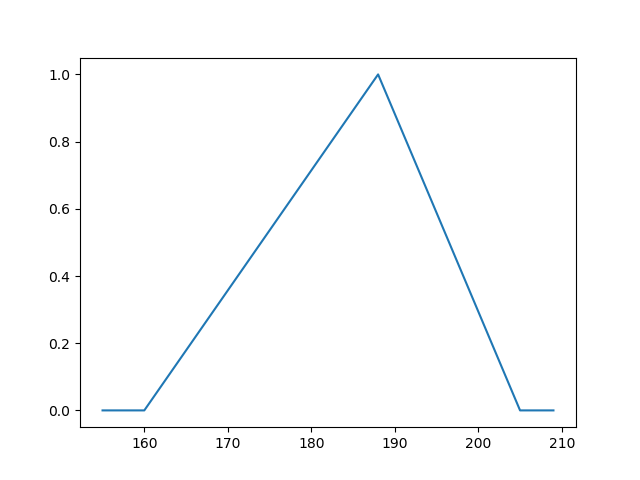
让我们再次使用 三角形，参数为 a = 160，b = 188，c = 205

5. 每场比赛助攻数（APG）

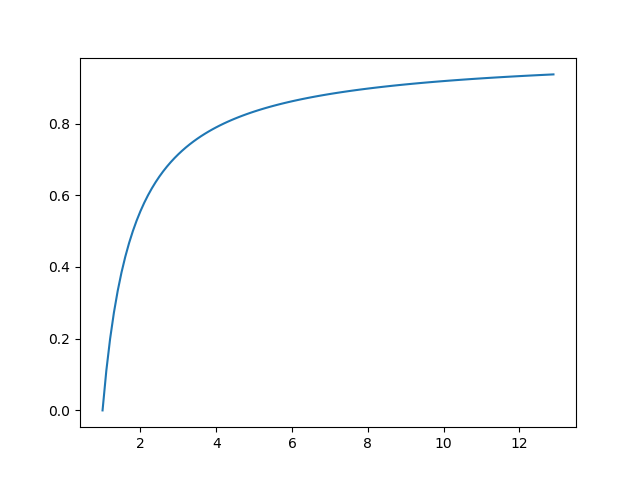
这里我们选择一些非基本的，自定义隶属度函数，它在y=1处有水平渐近线

这意味着函数在x=1处值为0，随着x的增加单调递增，永远不会等于1，因为函数有渐近线 y = 1。以下是这个图形的公式

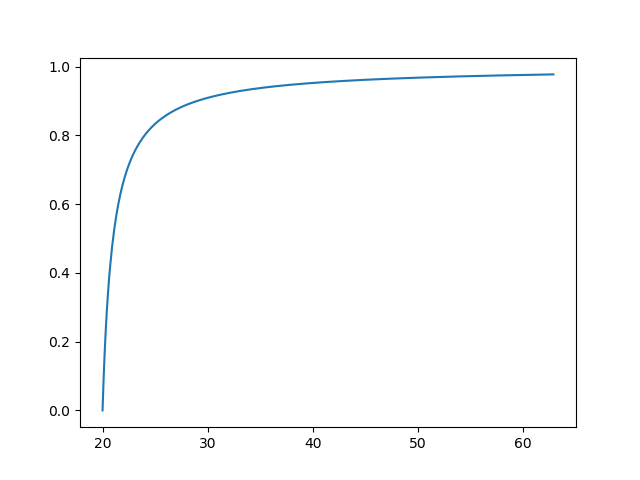
6. 三分命中率（3P%）

这里我们应该使用相同类型的函数，但参数不同。

聚合

让我们以JJ Barea为例，计算隶属函数的值。

因此，我们对每个特征都有评估，需要将它们聚合为单个评估。这里有许多聚合函数，但为了简单起见，我们可以只使用最著名的聚合函数——算术平均数

因此，JJ Barea的聚合评估会是：

完整的评估表看起来是这样的

实现

首先，让我们声明篮球运动员的特征

$age = new Feature('age', new Trapmf(18, 24, 26, 35));
$nbaYears = new Feature('nba_years', new Trimf(0, 5, 13));
$cost = new Feature('cost', new Trimf(0, 13, 20));
$height = new Feature('height', new Trimf(160, 188, 205));

这个库已经包含了三角形和梯形隶属函数的实现，因此这些类被用于此代码中。但是，如上所述，我们有两种具有水平渐近线的自定义函数，用于APG和3P%。因此，我们可以通过仅实现MembershipFunction接口来创建我们的自定义隶属函数

class Assists implements MembershipFunction
{
    function call($x)
    {
        $x = (float)$x;

        return ($x - 1) / ($x - 0.2);

    }
}

class TPP implements MembershipFunction
{

    function call($x)
    {
        $x = (float)$x;

        return ($x - 20) / ($x - 19);
    }
}

并声明相关特征

$assistsPerGame = new Feature('apg', new Assists());
$threePointPercentage = new Feature('3pp', new TPP());

创建特征数组

$features = array(
    $age,
    $nbaYears,
    $cost,
    $height,
    $assistsPerGame,
    $threePointPercentage
);

守门员数组

$guards = array(
    new Item($identifier = 'Milos Teodosic',
        $feature_values = array(
            'age' => 31,
            'height' => 196,
            '3pp' => 37.9,
            'apg' => 4.6,
            'nba_years' => 0,
            'cost' => 12.2
        )),
    new Item($identifier = 'Isaiah Thomas',
        $feature_values = array(
            'age' => 29,
            'height' => 175,
            '3pp' => 36.1,
            'apg' => 5.1,
            'nba_years' => 4,
            'cost' => 19.8
        )),
    new Item($identifier = 'JJ Barea',
        $feature_values = array(
            'age' => 33,
            'height' => 182,
            '3pp' => 35.4,
            'apg' => 3.9,
            'nba_years' => 11,
            'cost' => 9.2
        )),
    new Item($identifier = 'Ricky Rubio',
        $feature_values = array(
            'age' => 27,
            'height' => 193,
            '3pp' => 32.5,
            'apg' => 7.9,
            'nba_years' => 6,
            'cost' => 16
        )),
    new Item($identifier = 'Alexey Shved',
        $feature_values = array(
            'age' => 29,
            'height' => 198,
            '3pp' => 30.6,
            'apg' => 2.5,
            'nba_years' => 3,
            'cost' => 8
        ))
);

并分析这些数据

$analyzer = new Analyzer($features, $guards, new ArithmeticMean());
$analyzer->analyze();
$sorted = $analyzer->sort();

输出

foreach ($sorted as $item)
{
    echo $item->item_identifier." - ".$item->score."\n";
}

输出

Ricky Rubio - 0.81053827254808
Alexey Shved - 0.64329716740423
Isaiah Thomas - 0.6348679237777
JJ Barea - 0.61473949827608
Milos Teodosic - 0.61293158548061

优先级...权重...

我们可以预期，我们可能不想让所有特征都具有相同的重要性。例如，你可能只需要一个赛季的球员，球员的年龄并不重要，但也不是太不重要。因此，我们可以将权重设置为[0,1]的范围

$age->set_weight(0.4);
$nbaYears->set_weight(0.2);
$height->set_weight(0.8);
$cost->set_weight(1);
$assistsPerGame->set_weight(0.71);
$threePointPercentage->set_weight(0.77);

$analyzer = new Analyzer($features, $guards, new WeightedArithmeticMean());
$analyzer->analyze();
$sorted = $analyzer->sort();

并检查设置权重后输出如何变化

Ricky Rubio - 0.78430304749612
Milos Teodosic - 0.68180312874937
JJ Barea - 0.67695882586768
Alexey Shved - 0.64070029059168
Isaiah Thomas - 0.58441672648242

看起来Ricky Rubio根据我们的需求和优先级对我们来说是不具有竞争力的优秀球员，但在设置优先级后，Rubio之后的顺序发生了变化，Milos Teodosic成为了Rubio之后最受欢迎的球员。

反馈和Pull Requests

任何类型的Pull Requests都将被接受。

注意： 有少量的隶属函数和聚合函数，我认为最期望的Pull Requests将是关于它们的

C#版本

https://github.com/goodot/fuzzy-decision-maker

(尚未完成)