README

介绍
许可协议
安装
图类型
图的表示
- 有向图
  - 有向无权图
  - 有向加权图
- 无向图
  - 无向无权图
  - 无向加权图
图API
使用算法

介绍

此存储库包含各种图算法的实现。

许可协议

本代码在以下许可协议下发布

创意共享署名-非商业4.0国际（CC BY-NC 4.0）

查看文件LICENSE.TXT

安装

从命令行

composer require dbeurive/graph

或，在文件composer.json内

"require": {
    "dbeurive/graph": "*"
}

图类型

图可能是

有向或无向。
加权或无权。

给定的图可能是

图的表示

可以使用多种形式来表示图。例如

边列表
邻接矩阵
邻接表

本文档介绍了表示图的多种方式

https://fr.khanacademy.org/computing/computer-science/algorithms/graph-representation/a/representing-graphs

此PHP模块使用称为“邻接表”的公理化。

有向图

顶点有后继（和前驱）。

我们可以选择通过后继列表或前驱列表来描述图。

有向无权图

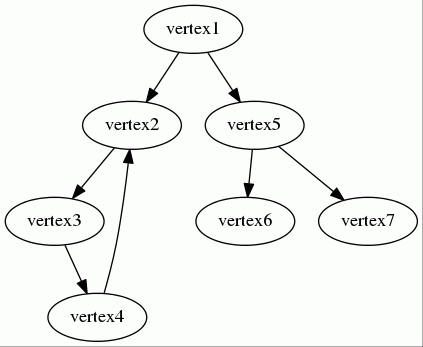
让我们考虑以下有向无权图

关联数组可以表示为以下关联数组

array(
    'vertex1' => array('vertex2' => null, 'vertex5' => null),
    'vertex5' => array('vertex6' => null, 'vertex7' => null),
    'vertex2' => array('vertex3' => null),
    'vertex3' => array('vertex4' => null),
    'vertex4' => array('vertex2' => null)
)

或CSV文件

vertex1 vertex2 vertex5
vertex5 vertex6 vertex7
vertex2 vertex3
vertex3 vertex4
vertex4 vertex2

顶点vertex1有两个后继：vertex2和vertex5。
顶点vertex2有一个后继：vertex3。
...

见此示例。

有向加权图

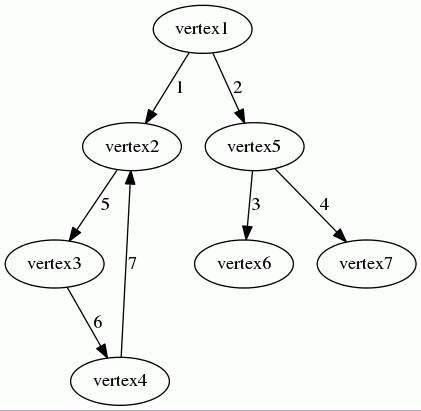
让我们考虑以下有向加权图

关联数组可以表示为以下关联数组

array(
    'vertex1' => array('vertex2' => 1, 'vertex5' => 2),
    'vertex5' => array('vertex6' => 3, 'vertex7' => 4),
    'vertex2' => array('vertex3' => 5),
    'vertex3' => array('vertex4' => 6),
    'vertex4' => array('vertex2' => 7)
)

或CSV文件

vertex1 vertex2:1 vertex5:2
vertex5 vertex6:3 vertex7:4
vertex2 vertex3:5
vertex3 vertex4:6
vertex4 vertex2:7

顶点vertex1有两个后继：vertex2和vertex5。
- 从vertex1到vertex2的边的权重为1。
- 从vertex1到vertex5的边的权重为2。
顶点vertex2有一个后继：vertex3。
- 从vertex2到vertex3的边的权重为5。
...

请参阅此示例。

无向图

顶点有邻居。

无向且无权

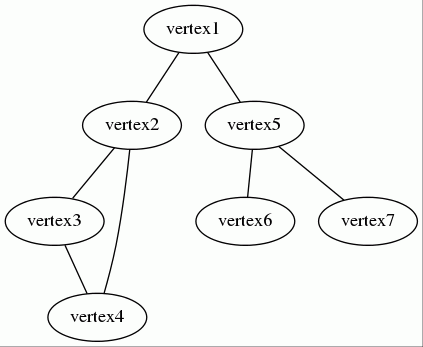
让我们考虑以下无向无权图

关联数组可以表示为以下关联数组

array(
    'vertex1' => array('vertex2' => null, 'vertex5' => null),
    'vertex5' => array('vertex6' => null, 'vertex7' => null),
    'vertex2' => array('vertex3' => null),
    'vertex3' => array('vertex4' => null),
    'vertex4' => array('vertex2' => null)
);

或通过CV文件

vertex1 vertex2 vertex5
vertex5 vertex6 vertex7
vertex2 vertex3
vertex3 vertex4
vertex4 vertex2

顶点 vertex1 有两个邻居： vertex2 和 vertex5。
顶点 vertex1 有两个邻居： vertex6 和 vertex7。
...

请参阅此示例。

无向且有向

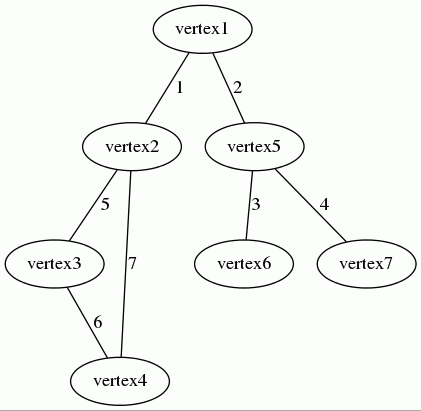
让我们考虑以下无向加权图

关联数组可以表示为以下关联数组

array(
    'vertex1' => array('vertex2' => 1, 'vertex5' => 2),
    'vertex5' => array('vertex6' => 3, 'vertex7' => 4),
    'vertex2' => array('vertex3' => 5),
    'vertex3' => array('vertex4' => 6),
    'vertex4' => array('vertex2' => 7)
);

或通过CSV文件

vertex1 vertex2:1 vertex5:2
vertex5 vertex6:3 vertex7:4
vertex2 vertex3:5
vertex3 vertex4:6
vertex4 vertex2:7

顶点vertex1有两个后继：vertex2和vertex5。
- 从vertex1到vertex2的边的权重为1。
- 从vertex1到vertex5的边的权重为2。
顶点vertex2有一个后继：vertex3。
- 从vertex2到vertex3的边的权重为5。
...

请参阅此示例。

图API

介绍

图的API允许以下操作

从CSV文件加载图。
将图转储到CSV文件。
创建图的GraphViz表示。
"完成"图的表示。
对于有向图：从后继者的列表计算前驱者的列表，反之亦然。

而不是详细描述API，我们将展示使用示例。

可以使用phpDocumentor生成详细的API描述。只需转到此包的根目录并执行以下命令：phpdoc。文档将在doc/api目录内生成。

从CSV文件加载图

使用默认加载器加载CSV

摘要

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->loadSuccessorsFromCsv($csvSuccessorsPath);
$graph->loadPredecessorsFromCsv($csvPredecessorsPath);

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->loadNeighboursFromCsv($csvSuccessorsPath);

默认情况下

字段由空格分隔。
边的权重由冒号字符表示。
顶点名称按原样加载。

标准CSV文件的示例

vertex1
vertex2 vertex1 vertex4
vertex5 vertex1
vertex6 vertex5
vertex7 vertex5
vertex3 vertex2
vertex4 vertex3

或

vertex1
vertex2 vertex1:1 vertex4:7
vertex5 vertex1:2
vertex6 vertex5:3
vertex7 vertex5:4
vertex3 vertex2:5
vertex4 vertex3:6

请参阅示例from-csv-directed-unweighted.php。

请参阅示例from-csv-directed-weighted.php。

请参阅示例from-csv-undirected-unweighted.php。

请参阅示例from-csv-undirected-weighted.php。

使用自定义加载器加载CSV

摘要

$graph = new DirectedUnweighted(); // or UndirectedUnweighted
$graph->setFieldSeparator(';');
$graph->setVertexUnserializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setLinePreProcessor(function($inLine) { return trim($inLine); });

$graph = new DirectedWeighted(); // or UndirectedWeighted
$graph->setFieldSeparator(';');
$graph->setVertexUnserializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setLinePreProcessor(function($inLine) { return trim($inLine); });
$graph->setWeightIndicator('::');

在加载CSV文件时，可以指定非标准属性

字段分隔符。默认字段分隔符是空格（" "）。
权重指示符（仅适用于加权图）。默认权重指示符是冒号字符（":"）。

还可以指定对以下数据的操作

顶点名称。
CSV行（例如，您可以删除前导和尾随空格）。

操作通过"可调用"（参见此说明）指定。

在以下示例中

我们更改了字段分隔符（我们使用";"而不是" "）。
我们更改了权重指示符（我们使用"::"而不是":")。
我们将顶点名称转换为大写。
在执行任何其他操作之前，我们删除了每行的前导和尾随空格。

请参阅示例from-csv-directed-unweighted-non-standard.php。

请参阅示例from-csv-directed-weighted-non-standard.php。

将图转储到CSV文件

使用默认转储器转储到CSV

摘要

$graph = new DirectedUnweighted();        // Or DirectedWeighted
$graph->setSuccessors($listOfSuccessors); // You can also set the lists of predecessors.
$graph->dumpSuccessorsToCsv($csvPath);    // You can also dump the lists of predecessors.

$graph = new UndirectedUnweighted();      // Or UndirectedWeighted
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

查看示例 to-csv-directed-unweighted.php。

查看示例 to-csv-directed-weighted.php。

查看示例 to-csv-undirected-unweighted.php。

查看示例 to-csv-undirected-weighted.php。

使用自定义的导出器将数据导出到CSV

摘要

// Directed Weighted

$graph = new DirectedWeighted();
$graph->setSuccessors($listOfSuccessors);
$graph->calculatePredecessorsFromSuccessors();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setWeightIndicator('::');
$graph->dumpSuccessorsToCsv($csvPath);
$graph->dumpPredecessorsToCsv($csvPath);

// Directed Unweighted

$graph = new DirectedUnweighted();
$graph->setSuccessors($listOfSuccessors);
$graph->calculatePredecessorsFromSuccessors();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function($inVertex) { return strtoupper($inVertex); });
$graph->dumpSuccessorsToCsv($csvPath);
$graph->dumpPredecessorsToCsv($csvPath);

// Undirected Weighted

$graph = new UndirectedWeighted();
$graph->setFieldSeparator(';');
$graph->setWeightIndicator('::');
$graph->setVertexSerializer(function ($inVertex) { return strtoupper($inVertex); } );
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

// Undirected Unweighted

$graph = new UndirectedUnweighted();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function ($inVertex) { return strtoupper($inVertex); } );
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

在导出CSV文件时，可以指定非标准的属性

字段分隔符。默认字段分隔符是空格（" "）。
权重指示符（仅适用于加权图）。默认权重指示符是冒号字符（":"）。

还可以指定对以下数据的操作

顶点名称。

操作通过"可调用"（参见此说明）指定。

查看示例 to-csv-directed-unweighted-non-standard.php。

查看示例 to-csv-directed-weighted-non-standard.php。

查看示例 to-csv-undirected-unweighted-non-standard.php。

查看示例 to-csv-undirected-weighted-non-standard.php。

将图导出到其GraphViz表示形式

摘要

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($listOfSuccessors);
$txt = $graph->dumpSuccessorsToGraphviz();
$graph->calculatePredecessorsFromSuccessors();
$txt = $graph->dumpPredecessorsToGraphviz();

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->setNeighbours($listOfNeighbours);
$txt = $graph->dumpNeighboursToGraphviz();

请注意，生成的GraphViz表示形式可高度自定义。方法 dumpSuccessorsToGraphviz、dumpPredecessorsToGraphviz 和 dumpNeighboursToGraphviz 接受参数。这些参数允许您自定义顶点和边的外观。

查看示例 to-graphviz-directed-unweighted.php。

查看示例 to-graphviz-directed-weighted.php。

查看示例 to-graphviz-undirected-unweighted.php。

查看示例 to-graphviz-undirected-weighted.php。

使用算法

"广度优先搜索"算法

请参阅此处的描述。

概要

$vertices = array();

// Define a callback that will be executed for each visited vertex.
// * If the function returns true, then the exploration of the graph continues.
// * If the function returns false, then the exploration of the graph ends.

$callback = function($inVertex) use(&$vertices) {
    $vertices[] = $inVertex;
    return true;
};

// For directed graphs

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($successors, true);
$graph->calculatePredecessorsFromSuccessors();
$algo = new DirectedBreadthFirstSearch($graph, $callback);
$algo->followSuccessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the sucessors.
$algo->followPredecessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the predecessors.

// For undirected graphs

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->setNeighbours($successors, true);
$algorithm = new UndirectedBreadthFirstSearch($graph, $callback);
$algorithm->run('e1', $callback); // Start traversing the graph.

请注意，此算法适用于有向和无向图。

请注意，回调函数（$callback）返回的值决定了方法 run() 的行为。

如果回调函数返回值为true，则方法 run() 继续图的遍历。

如果回调函数返回值为false，则方法 run() 停止图的遍历。

查看示例 breadth-first-search-directed.php。

查看示例 breadth-first-search-undirected.php。

"深度优先搜索"算法

请参阅此处的描述。

概要

$vertices = array();

// Define a callback that will be executed for each visited vertex.
// * If the function returns true, then the exploration of the graph continues.
// * If the function returns false, then the exploration of the graph ends.

$callback = function($inVertex) use(&$vertices) {
    $vertices[] = $inVertex;
    return true;
};

// For directed graphs

$graph = new DirectedUnweighted(); // Or DirectedWeighted 
$graph->setSuccessors($successors, true);
$graph->calculatePredecessorsFromSuccessors();
$algo = new DirectedDepthFirstSearch($graph, $callback);
$algo->followSuccessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the successors.
$algo->followPredecessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the predecessors.

请注意，此算法适用于有向和无向图。

请注意，回调函数（$callback）返回的值决定了方法 run() 的行为。

如果回调函数返回值为true，则方法 run() 继续图的遍历。

如果回调函数返回值为false，则方法 run() 停止图的遍历。

查看示例 depth-first-search-directed.php。

查看示例 depth-first-search-undirected.php。

迪杰斯特拉算法

请参阅此处的描述。

此算法适用于有向和无向图。
图必须是带权重的。

概要

// With directed graphs

$graph = new DirectedWeighted();
$graph->setSuccessors($successors, true);
$algorithm = new DirectedDijkstra($graph);
$algorithm->followSuccessors();
$distances = $algorithm->run($vertexName); // Start the algorithm.
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

// With undirected graphs

$graph = new UndirectedWeighted();
$graph->setNeighbours($neighbours, true);
$algorithm = new UndirectedDijkstra($graph);
$distances = $algorithm->run($vertexName);
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

查看示例 dijkstra-directed.php。

查看示例 dijkstra-undirected.php。

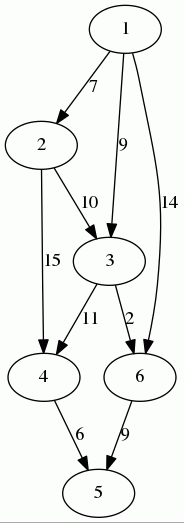
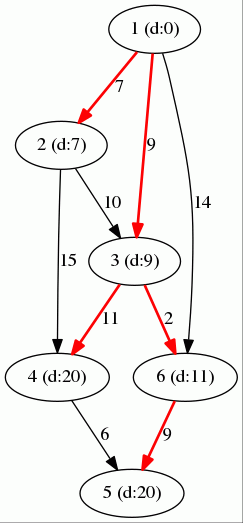
示意图

给定以下图，让我们找到从顶点 "1" 到所有其他顶点的最短路径。

运行算法后，我们得到

顶点 "1" 和顶点 "3" 之间的最短距离是 9。
顶点 "1" 和顶点 "6" 之间的最短距离是 11。
顶点 "1" 和顶点 "5" 之间的最短距离是 20。
...

最短路径用红色打印。

Tarjan 算法

请参阅此处的描述。

此算法仅适用于有向图。
图可以是加权的，也可以不是。

概要

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($successors, true);

$algorithm = new DirectedTarjan($graph);
$algorithm->followSuccessors();
$scc = $algorithm->run();
$cycles = $algorithm->getCycles();
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

查看示例 tarjan.php。

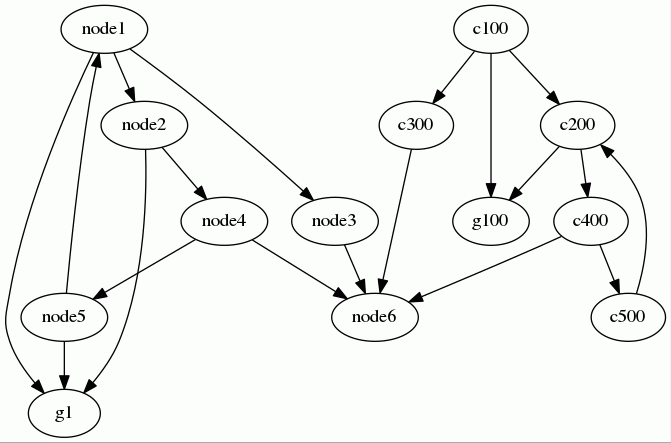
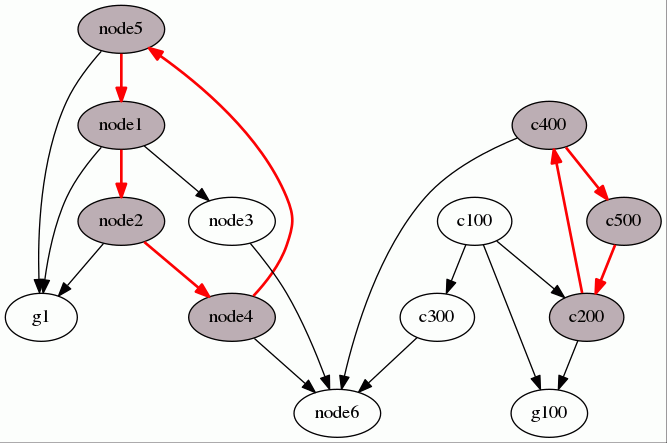
示意图

给定以下图，让我们找到所有环

运行算法后，我们得到

请注意，此算法不会返回图内环的列表。它返回的是强连通分量的列表。然而，环检测是此算法的应用之一。在这里，我们选择展示 getCycles() 方法的结果。

dbeurive / graph

维护者

详细信息

README

介绍

许可协议

安装

图类型

图的表示

有向图

有向无权图

有向加权图

无向图

无向且无权

无向且有向

图API

介绍

从CSV文件加载图

使用默认加载器加载CSV

使用自定义加载器加载CSV

将图转储到CSV文件

使用默认转储器转储到CSV

使用自定义的导出器将数据导出到CSV

将图导出到其GraphViz表示形式

使用算法

"广度优先搜索"算法

概要

"深度优先搜索"算法

概要

迪杰斯特拉算法

概要

示意图

Tarjan 算法

概要

示意图